Plan familiar psicológico contra el coronavirus

Geometría plana

La geometría es la rama de la matemática orientada al análisis de las medidas y de las propiedad de las figuras en un espacio o en un plano.

La geometría plana es una parte de la geometría que trata de aquellos elementos cuyos puntos están contenidos en un plano, y estos elementos geométricos son estudiados a partir de dos dimensiones.

Los elementos básicos con los que se suele trabajar en esta parte de geometría son: el punto, la recta, semirrecta, segmento, así como otros conceptos que se irán desarrollando en los siguientes apartados.

                                                   

Ángulos

Ángulos.

En geometría, el ángulo puede ser definido como la parte del plano determinada por dos semirrectas, llamadas lados que tienen el mismo punto de origen llamado vértice del ángulo.

La medida de un ángulo es considerada como la longitud del arco de circunferencia centrada en el vértice y delimitada por sus lados. Su medida es un múltiplo de la razón entre la longitud del arco y el radio. Su unidad natural es el radian, pero también se puede utilizar el grado sexagesimal o el grado centesimal.

Ángulos adyacentes.

Los ángulos adyacentes son aquellos ángulos que tiene el vértice y un lado en común, al tiempo que sus otros dos lados son semirrectas opuestas a veces pueden tener hasta 4 lados, dependiendo de los vértices. de allí resulta que los ángulos adyacentes son a la vez consecutivos y suplementarios, porque juntos equivalen a un angulo llano (180°) sin poseer ningún punto interior en común. 

Los senos de los ángulos adyacentes son lo mismo, por ejemplo:

sin( 120° ) = sin( 60° )

sin( α ) = sin( 180° - α )

sin( α ) = sin( π - α )

Ángulos obtusos.

El ángulo obtuso es el espacio entre dos rectas que comparten un mismo vértice cuya inclinación o abertura es mayor que 90 grados (90°)  y menor que 180 grados (180°).

Ángulo recto.

Un ángulo recto es aquel que mide 90°. Su amplitud medida en otras unidades es:  π/ 2 radianes y 100°(centesimales). Sus dos lados son dos semirrectas perpendiculares y el vértice es el origen de dichas semirrectas. 

Ángulo agudo.

El ángulo agudo es el espacio entre dos rectas que comparten un mismo vértice cuya inclinación o apertura es mayor que 0 grados (0°) y menor que 90 grados (90°). 

 

Ángulos complementarios. 

Los ángulos complementarios son aquellos ángulos cuyas medidas suman 90° sexagesimales, es decir, que si dos ángulos complementarios son a su vez consecutivos, los lados no comunes de estos forman un ángulo recto. 

Ángulos suplementarios.

Dos ángulos  y   son ángulos suplementarios, si suman 180°.

Método de obtención.

Para obtener el ángulo suplementario  de un determinado ángulo  se restara  a 180° de la siguiente manera

     =180°- 

 

Características de los triángulos (según sus lados)

Estos se clasifican en los siguientes 3 tipos de triángulos, que son:

Triángulo equilatero.

Este triángulo es un polígono regular, esto quiere decir que posee tres lados iguales, los triángulos equilateros son también triángulos equiángulares, esto quiere decir que los 3 ángulos internos son iguales y miden 60°.

Triángulo isósceles.

Un triángulo es un tipo de triángulo que tiene dos lados de igual longitud. A veces se especifica que tiene dos y solo dos lados de igualmente longitud.el ángulo formado por los lados de igual longitud se llama ángulo en el vértice y el lado opuesto a el, base.

Triángulo escaleno.

Todos sus lados son de distintas medidas y tiene tres ángulos de diferentes medidas.

Características de los triángulos(según sus ángulos)

Triángulo acutángulo.

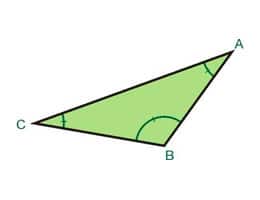
Este triángulo tiene la característica de que posee tres ángulos agudos. estos ángulos agudos miden menos de 90°.

Triángulo obtusángulo.

Este triángulo tiene la característica de que posee dos ángulos agudos y uno obtuso. Los dos ángulos agudos que miden menos de 90° y uno obtuso que mide más de 90°.

Triángulo rectángulo.

Este triángulo tiene la característica de que posee un ángulo recto y dos agudos. El angulo recto que mide 90° y los otros dos ángulos agudos que miden menos de 90°.

Rectas (paralelas, perpendiculares)

Rectas.

Una recta es una sucesión infinita de puntos, situados todos en una misma dirección, en tanto, esa sucesión se caracteriza por ser continua e indefinida.

Rectas paralelas.

Las rectas paralelas son aquellas lineas que mantienen una cierta distancia entre sí, y a pesar de prolongar su trayectoria hasta el infinito, nunca se encuentran o se tocan en ningún punto; es decir se entiende por rectas paralelas las que se hallan en un mismo plano, no presentan ningún punto en común y muestran la misma pendiente, o sea que no han de tocarse ni cruzarse, ni siquiera sus prolongaciones se cruzan, un claro ejemplo de esto son las vías del tren.

Rectas perpendiculares.

Las rectas perpendiculares son dos o más rectas que se interceptan formando un ángulo de 90° como las dos rectas dibujadas en la gráfica.

Trigonometría

La trigonometría es una rama de la matemática, cuyo significado etimológico es 'la medición de los triángulos'.  En términos generales, la trigonometría es el estudio de las razones trigonométricas por ejemplo: seno, coseno, tangente, cotangente, secante y cosecante.